卷积神经网络研究综述

一、神经网络基础

1.1 神经元

神经元是人工神经网络的基本处理单元，一般是 多输入单输出 的单元，其结构模型如下图所示。

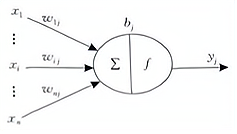
各参数含义为：

• $x_i$：表示输入信号，n 个输入信号同时输入神经元 ｊ；
• $w_{ij}$：表示输入信号 $x_i$ 与神经元 j 连接的权重值；
• $b_j$：表示神经元的内部状态即偏置值；
• $y_j$：神经元的输出。

输入与输出之间的对应关系可表示为：

$y_j=f(b_j+\sum\limits_{i=1}^{n}(x_i \times w_{ij}))$

$f(\cdot)$ 为激活函数，其可以有多种选择，包括 ReLU、sigmoid、tanh 等。

1.2 多层感知器

多层感知机（Multilayer Perceptron，MLP）是由 输入层、隐含层（一层或多层）及输出层 构成的神经网络模型，它可以解决单层感知机不能解决的线性不可分问题。下图是含有 2 个隐含层的多层感知机网络拓扑结构图。

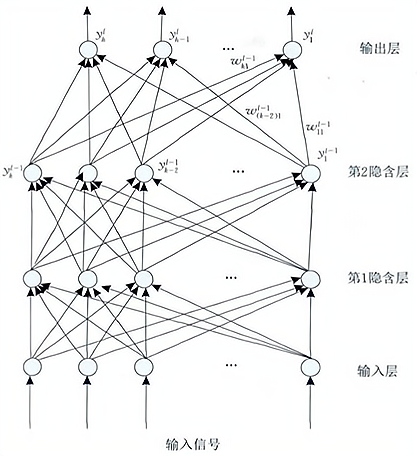
输入层神经元接收输入信号，隐含层和输出层的每一个神经元与之相邻层的所有神经元连接，即 全连接，同一层的神经元间不相连。

当多层感知器用于分类时，其输入神经元个数为输入信号的维数，输出神经元个数为类别数，隐含层个数及隐层神经元个数视具体情况而定。但在实际应用中，由于受到参数学习效率影响，一般使用不超过 ３ 层的浅层模型。

BP 算法可分为两个阶段：前向传播和后向传播，其后向传播始于 MLP 的输出层。以上图为例，则损失函数为：

$E=E(y_1^l,\cdots,y_h^l)=\sum\limits_{j=1}^h(y_j^l-t_j)^2$

其中第 $l$ 层为输出层，$t_j$ 为输出层第 $j$ 个神经元的期望输出，对损失函数求一阶偏导，则网络权值更新公式为：

$\omega_{im}^{l-1}=\omega_{im}^{l-1}-\eta\times\frac{\partial{E}}{\partial{\omega_{im}^{l-1}}}$

其中，$\eta$ 为学习率。

二、CNN 概述

CNN 的基本结构由 输入层、卷积层（convolutional layer）、池化层（pooling layer，也称为取样层）、全连接层及输出层 构成。卷积层和池化层一般会取若干个，采用卷积层和池化层交替设置，即一个卷积层连接一个池化层，池化层后再连接一个卷积层，依此类推。

由于卷积层中输出特征图的每个神经元与其输入进行局部连接，并通过对应的连接权值与局部输入进行加权求和再加上偏置值，得到该神经元输入值，该过程等同于卷积过程，CNN 也由此而得名。

2.1 卷积层

卷积层由多个 特征图（Feature Map） 组成，每个特征图由多个神经元组成，它的每一个神经元通过卷积核与上一层特征图的局部区域相连。

CNN 的卷积层通过卷积操作提取输入的不同特征，第 1 层卷积层提取低级特征如边缘、线条、角落，更高层的卷积层提取更高级的特征。下图为一维 CNN 的卷积层和池化层结构示意图，最顶层为池化层，中间层为卷积层，最底层为卷积层的输入层。

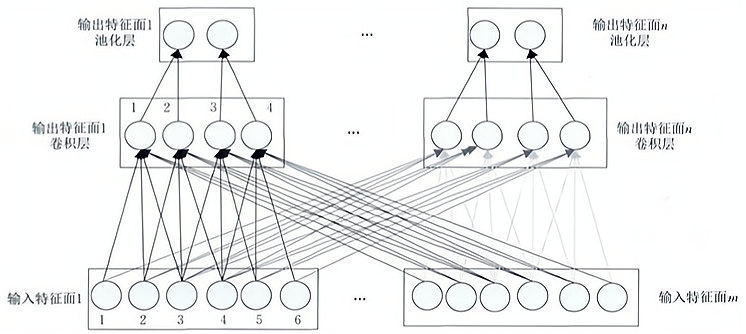
可看出卷积层的神经元被组织到各个特征图中，每个神经元通过一组权值被连接到上一层特征图的局部区域，即 卷积层中的神经元与其输入层中的特征图进行局部连接，然后将该局部加权和传递给一个非线性函数如 ReLU 函数即可获得卷积层中每个神经元的输出值。

在同一个输入特征图和同一个输出特征图中，CNN 的 权值共享。通过权值共享可以减小模型复杂度，使得网络更易于训练。以上图为例，

$\omega_{1(1)1(1)}=\omega_{1(2)1(2)}=\omega_{1(3)1(3)}=\omega_{1(4)1(4)}$

而

$\omega_{1(1)1(1)}\neq\omega_{1(2)1(1)}\neq\omega_{1(3)1(1)}$

其中 $\omega_{m(i)n(j)}$ 表示输入特征图 m 第 i 个神经元与输出特征图 n 第 j 个神经元的连接权重。

此外，卷积核的 滑动步长 即卷积核每一次平移的距离也是卷积层中一个重要的参数，CNN 中每一个卷积层的每个输出特征图的大小（即神经元的个数）$oMapN$ 满足如下关系：

$oMapN=\frac{iMapN-CWindow}{cInterval}+1$

其中，$iMapN$ 表示每一个输入特征图的大小；$CWindow$ 为卷积核的大小；$CInterval$ 表示卷积核在其上一层的滑动步长。通常情况下，要保证上式能够整除，否则需对 CNN 网络结构做额外处理。

每个卷积层可训练参数数目 $CParams$ 满足：

$CParams=(iMap \times CWindow + 1)\times oMap$

其中，$oMap$ 为每个卷积层输出特征图的个数；$iMap$ 为输入特征图的个数；$1$ 表示偏置，在同一个输出特征图中偏置也共享。

假设卷积层中输出特征图 n 第 k 个神经元的输出值为 $x_{nk}^{\rm out}$，而 $x_{mh}^{\rm in}$ 表示其输入特征图 m 第 h 个神经元的输出值，以上图为例，则

$x_{nk}^{\rm out}=f_{\rm cov}(x_{1h}^{\rm in}\times \omega_{1(h)n(k)}+x_{1(h+1)}^{\rm in}\times \omega_{1(h+1)n(k)}+x_{1(h+2)}^{\rm in}\times \omega_{1(h+2)n(k)}+\cdots+b_n)$

其中，$b_n$ 为输出特征图 n 的偏置值；$f_{\rm cov}(\cdot)$ 为非线性激活函数。

在传统的 CNN 中，激活函数一般使用饱和非线性函数（saturating nonlinearity）如 sigmoid、tanh 等。相比于饱和非线性函数，不饱和非线性函数（non-saturating nonlinearity）能够解决梯度爆炸/梯度消失问题，同时也能够加快收敛速度。因此在目前的 CNN 结构中常用不饱和非线性函数作为卷积层的激活函数如 ReLU 函数，ReLU 函数的计算公式如下所示：

$f_{\rm cov}(x)=\max(0,x)$

影响 CNN 性能的 ３ 个因素

1. 层数：增加网络的深度能够提升准确率；
2. 特征图的数目：增加特征图的数目也可以提升准确率；
3. 网络组织：增加一个卷积层比增加一个全连接层更能获得一个更高的准确率。

深度网络结构的 2 个优点

1. 可以促进特征的重复利用；
2. 能够获取高层表达中更抽象的特征，从而进行更抽象的表达。

2.2 池化层

池化层紧跟在卷积层之后，同样由多个特征图组成，它的每一个特征图唯一对应于其上一层的一个特征图，不会改变特征图的个数。

池化层旨在通过 降低特征图的分辨率 来获得具有空间不变性的特征。池化层起到二次提取特征的作用，它的每个神经元对局部接受域进行池化操作，常用的池化方法有最大池化、均值池化等。

通常所采用的池化方法中，池化层的同一个特征图不同神经元与上一层的局部接受域不重叠，然而也可以采用 重叠池化 的方法。所谓重叠池化方法就是相邻的池化窗口间有重叠区域，与无重叠池化相比，其泛化能力更强，更不易产生过拟合。

设池化层中第 n 个输出特征图第 l 个神经元的输出值为 $t_{nl}^{\rm out}$，以上图为例，则有：

$t_{nl}^{\rm out}=f_{\rm sub}(t_{nq}^{\rm in},t_{n(q+1)}^{\rm in})$

其中，$t_{nq}^{\rm in}$ 表示池化层的第 n 个输入特征图第 q 个神经元的输出值；$f_{\rm sub}(\cdot)$ 可为取最大值函数、取均值函数等。

池化层在上一层滑动的窗口也称为池化核，CNN 中每个池化层的每一个输出特征图的大小（神经元个数）$DoMapN$ 为：

$DoMapN=\frac{oMapN}{DWindow}$

其中，池化核的大小为 $DWindow$，上图中 $DWindow=2$。

池化层通过减少卷积层间的连接数量，即通过池化操作使神经元数量减少，降低了网络模型的计算量。

2.3 全连接层

在 CNN 结构中，经多个卷积层和池化层后，连接着 1 个或 1 个以上的全连接层。与 MLP 类似，全连接层中的每个神经元与其前一层的所有神经元进行全连接。全连接层可以 整合卷积层或者池化层中具有类别区分性的局部信息。

为了提升 CNN 网络性能，全连接层每个神经元的激活函数一般采用 ReLU 函数，最后一层全连接层的输出值被传递给一个输出层，可以采用 softmax 逻辑回归（softmax regression）进行分类，该层也可称为 softmax 层（softmax layer）。

为了避免训练过拟合，常在全连接层中采用正则化方法 —— dropout 技术，即使隐层神经元的输出值以 0.5 的概率变为 0，通过该技术部分隐层节点失效，这些节点不参加 CNN 的传播过程。由于一个神经元不能依赖于其它特定神经元而存在，所以这种技术 降低了神经元间相互适应的复杂性，使神经元学习能够得到 更鲁棒的特征。

2.4 特征图

特征图数目作为 CNN 的一个重要参数，它通常是根据实际应用进行设置的，如果特征图个数过少，可能会使一些有利于网络学习的特征被忽略掉，从而不利于网络的学习；但如果特征图个数过多，可训练参数个数及网络训练时间也会增加，这同样不利于学习网络模型。

通过实验发现：与每层特征图数目均相同的 CNN 结构相比，金字塔架构（该网络结构的特征图数目按倍数增加）更能有效利用计算资源。

目前，对于 CNN 网络特征图数目的设定通常采用的是人工设置方法，然后进行实验并观察所得训练模 型的分类性能，最终根据 网络训练时间 和 分类性能 来选取特征图数目。

2.5 与传统的模式识别算法相比

CNN 本质就是 每一个卷积层包含一定数量的特征图或者卷积核。与传统 MLP 相比：

• CNN 中卷积层的 权值共享 降低了网络模型复杂度，减少过拟合，从而获得了一个更好的泛化能力；
• CNN 中使用 池化操作 使模型中的神经元个数大大减少，对输入空间的平移不变性也更具鲁棒性；
• CNN 结构的 可扩展性 很强，可以采用很深的层数，深度模型具有更强的表达能力，能够处理更复杂的分类问题。

三、CNN 的一些改进算法

3.1 网中网结构

CNN 中的卷积滤波器是一种广义线性模型（Generalized Linear Model，GLM），GLM 的抽象水平比较低，但通过抽象却可以得到 对同一概念的不同变体保持不变的特征。

网中网（Network in Network，NIN）模型使用 微型神经网络（micro neural network）代替传统 CNN 的卷积过程，同时还采用 全局平均池化层来替换传统 CNN 的全连接层，它可以增强神经网络的表达能力。

微型神经网络主要采用 MLP 模型，如上图所示，(a) 是传统 CNN 的线性卷积层，(b) 是 NIN 模型的非线性卷积层，用 MLP 来取代原来的 GLM。这样通过引入非线性映射可以 提高模型对特征的抽象能力。

在传统的 CNN 结构中全连接层的参数过多，易于过拟合，因此它严重依赖于 dropout 正则化技术。NIN 模型采用全局平均池化来代替最后一个全连接层，能够 有效地减少参数量（没有可训练参数）。此外，全局平均池化对空间信息进行求和，因此 对输入的空间变化具有更强的鲁棒性。

3.2 空间变换网络

尽管 CNN 已经是一个能力强大的分类模型，但是它仍然会受到数据在 空间上多样性 的影响。

空间变换网络（Spatial Transformer Networks，STNs） 可以解决此问题，该模型由 3 个部分组成：本地化网络（localisation network）、网格生成器（grid generator）及采样器（sampler）。

STNs 可用于输入层，也可插入到卷积层或者其它层的后面，不需要改变原 CNN 模型的内部结构。STNs 能够 自适应地对数据进行空间变换和对齐，使得 CNN 模型对平移、缩放、旋转或者其他变换等保持不变性。此外，STNs 的 计算速度很快，几乎不影响原有 CNN 模型的训练速度。

3.3 反卷积

反卷积网络（Deconvolutional Networks） 与 CNN 的思想类似，只是运算上有所不同。

CNN 是一种自底而上的方法，其输入信号经过多层的卷积、非线性变换和下采样处理。而反卷积网络中的每层信息是 自顶而下 的，它对由已学习的滤波器组与特征面进行卷积后得到的特征求和就能重构输入信号。

四、实际应用

4.1 图像分类

AlexNet

• 采用 ReLU 代替饱和非线性函数 tanh，降低了模型的计算复杂度，训练速度也提升了几倍；
• 通过 dropout 技术在训练过程中将中间层的一些神经元随机置为 0，使模型更具鲁棒性，也减少了全连接层的过拟合；
• 还通过图像平移、图像水平镜像变换、改变图像灰度等方式 增加训练样本，从而减少过拟合。

GoogLeNet

• 大大 增加了 CNN 的深度，提出了一个超过 20 层的 CNN 结构；
• 采用了 3 中类型的卷积操作（$1 \times 1$，$3 \times 3$，$5 \times 5$），提升了计算机资源利用率（参数大大减少），且准确率更高；
• 在多个中间层中加入 监督信号，使网络结构得到有效训练。

VGG

• 通过在网络结构中 不断增加具有 $3 \times 3$ 卷积核的卷积层 来增加网络的深度，实验表明，当权值层数达到 16 ~ 19 时，模型性能能够得到有效提升；
• 用 具有小卷积核的多个卷积层替换一个具有较大卷积核的卷积层，这种替换方式减少了参数数量，也能够使决策函数更具判别性。

SPP-net

• 在 CNN 的最后一个卷积层与第 1 个全连接层中间加入一个空间金字塔池化（Spatial Pyramid Pooling，SPP）层，SPP 层能够使 CNN 不同大小的输入却产生大小相同的输出，打破了以往 CNN 模型输入均为固定大小的局限。

ResNet

• 主要特点是 跨层连接，通过引入捷径连接技术（shortcut connections）将输入跨层传递并与卷积的结果相加；
• 只有 一个池化层，它连接在最后一个卷积层后面，使得底层的网络能够得到充分训练，准确度也随着深度增加而显著提升。

说明

在层级很深的深度网络模型中，存在 梯度扩散 和 退化问题。

所谓退化问题就是：随着深度的增加，网络精度达到饱和，然后迅速下降，且该性能的下降不是由过拟合引起的，而是增加网络的深度使得它的训练误差也随之增加。

• 批规范化（Batch Normalization，BN） 是解决梯度扩散问题的一种有效方法。
• 可采用 残差网络（Residual Networks，ResNet） 来解决退化问题。

CNN 结构对比总结

1. 对于激活函数，可选取 没有 BN 的指数线性单元（Exponential Linear Unit，ELU） 或者 有 BN 的 ReLU 非线性函数；
2. 在池化层采用 平均池化及最大值池化之和 比随机池化、单独的平均池化或者最大池化等方法要好；
3. 相比较于平方根学习率衰减方法（square root）、平方学习率衰减方法（square）或者阶跃学习率衰减方法（step），使用 线性学习率衰减方法（linear） 更好；
4. 最小批量尺寸（mini-batch size）可取 128 或者 256，如果这对于所用 GPU 而言还是太大，那么可 按批量尺寸成比例减少学习率；
5. 目前深度学习的性能高度依赖数据集的大小，如果训练集大小小于它的最小值，那么模型性能会迅速降低，因此 当增加训练集大小时，需要检查数据量是否已达到模型所需的最小值；
6. 如果不能增加输入图像的大小，那么可以减小其后卷积层中的滑动步长，这样也能够得到大致相同的结果。

4.2 目标检测

YOLO

在 YOLO 中，将目标检测看成是一个 回归问题，输入整幅图像，并将图像划分为 $7 \times 7$ 个网格，通过 CNN 预测每个网格的多个包围盒（bounding boxes）及这些包围盒的类别概率。

• 优点
  • 将整幅图像作为下文信息，使得 背景误差比较小；
  • 检测速度非常快。
• 缺点
  • 因为每个网格只预测两个包围盒且只有一个类别，因此它具有很强的 空间约束性，这种约束 限制了模型对临近目标的预测，同时如果 小目标数量过多也会影响模型的检测能力；
  • 对于不包含在训练集中的目标或者有异常比例的目标，它的 泛化能力不是很好；
  • 模型的主要误差仍然因为是 不能精准定位 而引起的误差。

Faster R-CNN

Faster R-CNN 是 候选框网络（Region Proposal Network，RPN） 与 Fast R-CNN 结合并 共享卷积层特征 的网络，它也是基于分类器的方法。

SSD

SSD 利用了 YOLO 的 回归思想，同时还借鉴了 Faster R-CNN 的 锚点机制（anchor 机制）。

它与 YOLO 一样通过回归获取目标位置和类别，不同的是：SSD 预测某个位置采用的是该位置 周围的特征。最终，SSD 获得的检测精度与 Faster R-CNN 的差不多，但是 SSD 保持了 YOLO 快速检测的特性。

五、CNN 的优势

CNN 具有 4 个特点：局部连接、权值共享、池化操作 及 多层结构。

CNN 能够通过多层非线性变换，从数据中自动学习特征，从而代替手工设计的特征，且深层的结构使它具有 更强的表达能力和学习能力。在 CNN 中，通过增加深度从而增加网络的非线性来使它能够更好地拟合目标函数，获得更好的分布式特征。

六、展望

1. 目前所使用的 CNN 模型是 Hubel-Wiesel 模型简化的版本，有待 进一步借鉴 Hubel-Wiesel 模型，对它进行深入研究并发现结构特点及一些规律，同时还需 引入其他理论 使 CNN 能够充分发挥潜在的优势。
2. 对于一个具体的任务，仍很难确定使用哪种网络结构，使用多少层，每一层使用多少个神经元等才是合适的，仍然 需要详细的知识来选择合理的值 如学习率、正则化的强度等。
3. 如果训练数据集与测试数据集的分布不一样，则 CNN 也很难获得一个好的识别结果。因此，需要引入 CNN 模型的 自适应技术，可考虑将自适应抽样等应用于 CNN 模型中。
4. 尽管依赖于计算机的 CNN 模型是否与灵长类视觉系统相似仍待确定，但是通过 模仿和纳入灵长类视觉系统 也能使 CNN 模型具有进一步提高性能的潜力。

七、参考文献

• 《卷积神经网络研究综述》