跳跃表 SkipList

睡不醒的鲤鱼 2021-05-15 Redis Redis 原理

跳跃表「SkipList」是一种可以在有序元素中进行快速查找的数据结构，查找的时间复杂度可以达到 $O(logN)$ 。

跳跃表实现原理简单，性能却堪比平衡树。下面将详细讲解 SkipList 的实现。

# 一、基本思想

有序链表上的（近似）二分查找。

通过构建多级索引，用空间换时间，在上层索引查找，逐渐缩小范围，直至最底层索引定位到查找目标，

# 二、数据结构

Redis 的跳跃表由 server.h/zskiplistNode 和 serve.h/zskiplist 两个结构定义，其中 zskiplistNode 结构用于保存跳跃表节点的相关信息，比如节点的数量，以及指向表头节点和表尾节点的指针等等。

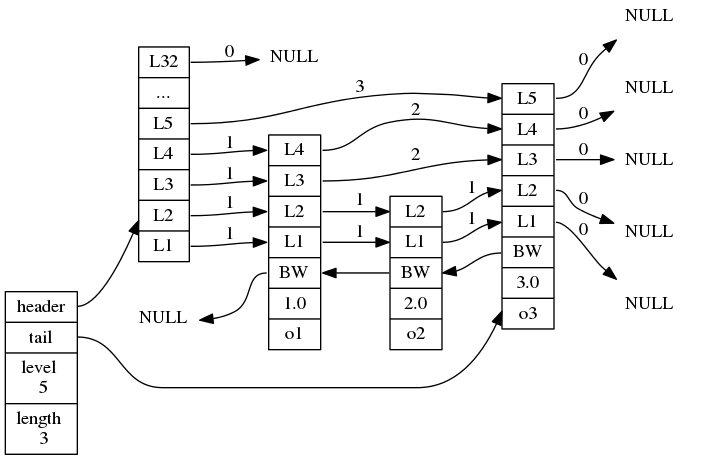
上图展示了一个跳跃表示例，位于图片最左边的是 zskiplist 结构，该结构包含以下属性：

header：指向跳跃表的表头节点；
tail：指向跳跃表的表尾节点；
level：记录目前跳跃表内，层数最大的那个节点的层数（不包含表头节点）；
length：记录跳跃表的长度，即跳跃表目前包含的节点数量（不包含表头节点）。

位于 zskiplist 结构右侧的是四个 zskiplistNode 结构，该结构包含以下属性：

level：层级，节点中用 $L_i$ 来标记节点的各个层，每个层都包含两个属性：前进指针和跨度，当程序从表头向表尾遍历时，访问会沿着当前层的前进指针进行；
backward：后退指针，上图节点中用 BW 字样标记，它指向当前节点的前一个节点，在程序从表尾向表头遍历时使用；
score：分值，在跳跃表中，节点按各自所保存的分值从小到大排列；
ele：成员对象，节点中用 $o_i$ 表示，用于存储字符串类型的数据。

接下来将对 zskiplistNode 和 zskiplist 两个结构进行详细介绍。

# 2.1 跳跃表节点

首先来看跳跃表节点的 zskiplistNode 结构体：

typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span;
    } level[];
} zskiplistNode;

1
2
3
4
5
6
7
8
9

该结构体包含以下属性：

ele：用于存储字符串类型的数据；
score：用于存储排序的分值；
backward：后退指针，指向当前节点最底层的前一个节点，从后向前遍历时使用；
level：柔性数组，每个节点的数组长度不一样，在生成跳跃表节点时，随机生成一个 1～64 的值，值越大出现的概率越低。

注意

level 数组的每项包含两个元素：

forward：指向本层下一个节点；
span：forward 指向的节点与本节点之间的元素个数，span 值越大，跳过的节点个数越多。

# 2.2 跳跃表

除了跳跃表节点外，还需要一个跳跃表结构来管理节点，Redis 使用 zskiplist 结构体，定义如下：

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

1
2
3
4
5

该结构体包含以下属性：

header：指向跳跃表头节点；
tail：指向跳跃表尾节点；
length：跳跃表长度，表示除头节点之外的节点总数；
level：跳跃表高度。

通过跳跃表结构体的属性我们可以看到，程序可以在 $O(1)$ 的时间内获取到跳跃表的头节点、尾节点、长度和高度。

# 三、基本操作

# 3.1 创建跳跃表

创建跳跃表节点

zskiplistNode *zslCreateNode(int level, double score, sds ele) {
    /* 申请内存为节点大小与柔性数组 level 大小之和 */
    zskiplistNode *zn =
        zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->ele = ele;
    return zn;
}

1
2
3
4
5
6
7
8

创建跳跃表步骤

zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;

    /* 创建头节点 */
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 3.2 插入节点

插入节点可分为以下几个步骤：

查找要插入的位置；
创建待插入节点；
插入节点并设置前后指针。

点击查看代码

/* Insert a new node in the skiplist. Assumes the element does not already
 * exist (up to the caller to enforce that). The skiplist takes ownership
 * of the passed SDS string 'ele'. */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {

    /* update：记录每一层与待插入节点相连的前一个节点
     * rank：记录每一层与头节点之间的路径的长度 */
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));

    /* 在各层查找节点的插入位置 */
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position
         * 记录到达待插入位置走过的距离，zsl->level-1 为头节点，初始化为 0，下面的每一层累加 rank
         * */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

        // 沿着前进指针遍历跳跃表
        // 向前移动条件：
        //   1. 下一个节点的 score 小于待插入节点的 score
        //   2. score 值相等，通过 sdscmp 方法比较 ele 值，ascii 值小的在前面
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            // 记录沿途跨过了多少个节点
            rank[i] += x->level[i].span;

            // 移动至下一个指针
            x = x->level[i].forward;
        }

        // 记录将要和新节点相连接的节点
        update[i] = x;
    }
    /* we assume the element is not already inside, since we allow duplicated
     * scores, reinserting the same element should never happen since the
     * caller of zslInsert() should test in the hash table if the element is
     * already inside or not.
     *
     * zslInsert() 的调用者会确保同分值且同成员的元素不会出现，
     * 所以这里不需要进一步进行检查，可以直接创建新元素。
     *
     * */

    // 获取一个随机值作为新节点的层数
    level = zslRandomLevel();

    // 如果新节点的层数比表中其他节点的层数都要大
    // 那么初始化表头节点中未使用的层，并将它们记录到 update 数组中
    // 将来也指向新节点
    if (level > zsl->level) {

        // 初始化未使用层
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }

        // 更新表中节点最大层数
        zsl->level = level;
    }

    // 创建新节点
    x = zslCreateNode(level,score,ele);

    // 将前面记录的指针指向新节点，并做相应的设置
    for (i = 0; i < level; i++) {

        // 设置新节点的 forward 指针
        x->level[i].forward = update[i]->level[i].forward;

        // 将沿途记录的各个节点的 forward 指针指向新节点
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        // 计算新节点跨越的节点数量
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 更新新节点插入之后，沿途节点的 span 值
        // 其中的 +1 计算的是新节点
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    // 未接触的节点的 span 值也需要增一，这些节点直接从表头指向新节点
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    // 设置新节点的后退指针
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;

    // 跳跃表的节点计数 +1
    zsl->length++;

    return x;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108

注意

根据源码可以看出，当 score 值相等时，跳跃表是按照 ele 值的字典序进行排序的。

在第二步创建节点时，需要随机生成节点的层高，Redis 正是通过这种随机化算法，保证高效的插入效率，下面来对这种算法进行简要分析。

节点层高的最小值为 1，最大值是 ZSKIPLIST_MAXLEVEL， Redis 6 中节点层高的值为 64。

#define ZSKIPLIST_MAXLEVEL 64

Redis 通过 zslRandomLevel 函数随机生成一个 1～64 的值，作为新建节点的高度，值越大出现的概率越低，节点层高确定之后便不会再修改。生成随机层高的代码如下：

#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */

int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

1
2
3
4
5
6
7
8

下面计算节点的期望层高，假设 p = ZSKIPLIST_P，则节点的期望层高为：

\begin{aligned} E &= 1\times{(1-p)}+2\times{p(1-p)}+3\times{p^2(1-p)}+\cdots \\ &= (1-p)\sum_{k=1}^{+\infty}kp^{k-1} \\ &= 1/(1-p) \end{aligned}

求和部分使用等比数列错位相减法~

当 p ＝ 0.25 时，跳跃表节点的期望层高为 $1/(1-0.25)\approx{1.33}$ 。

# 3.3 删除节点

删除节点可分为以下几个步骤：

查找需要更新的节点；
设置删除节点前后指针。

其中查找需要更新的节点要借助 update 数组，数组的赋值方式与插入节点前相同（参考 3.2 插入节点）。

点击查看代码

/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;

    // 更新所有和被删除节点 x 有关的节点的指针，解除它们之间的关系
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }

    // 更新被删除节点 x 的前进和后退指针
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }

    // 更新跳跃表最大层数（只在被删除节点是跳跃表中最高的节点时才执行）
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;

    // 跳跃表长度 -1
    zsl->length--;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 3.4 删除跳跃表

获取到跳跃表对象之后，从头节点的第 0 层开始，通过 forward 指针逐步向后遍历，每遇到一个节点便将释放其内存。

当所有节点的内存都被释放之后，释放跳跃表对象，即完成了跳跃表的删除操作。

点击查看代码

/* Free a whole skiplist. */
void zslFree(zskiplist *zsl) {
    zskiplistNode *node = zsl->header->level[0].forward, *next;

    zfree(zsl->header);
    while(node) {
        next = node->level[0].forward;
        zslFreeNode(node);
        node = next;
    }
    zfree(zsl);
}

1
2
3
4
5
6
7
8
9
10
11
12

# 四、跳跃表的应用

在 Redis 中，跳跃表主要应用于有序集合的底层实现（有序集合的另一种实现方式为压缩列表）。

Redis 的配置文件中关于有序集合底层实现有两个配置参数：

zset-max-ziplist-entries：zset 采用压缩列表时，元素个数最大值，默认值为 128。
zset-max-ziplist-value：zset 采用压缩列表时，每个元素的字符串长度最大值，默认值为 64。

zset 添加元素的主要逻辑位于 t_zset.c 的 zaddGenericCommand 函数中，zset 插入第一个元素时，会判断下面两种条件：

zset-max-ziplist-entries 的值是否等于 0；
zset-max-ziplist-value 是否小于要插入元素的字符串长度。

满足任一条件 Redis 就会采用跳跃表作为底层实现，否则采用压缩列表作为底层实现方式。

if (server.zset_max_ziplist_entries == 0 ||
    server.zset_max_ziplist_value < sdslen(c->argv[scoreidx+1]->ptr))
{
    zobj = createZsetObject();  // 创建跳跃表结构
} else {
    zobj = createZsetZiplistObject();  // 创建压缩列表结构
}

1
2
3
4
5
6
7

一般情况下，不会将 zset-max-ziplist-entries 配置成 0，元素的字符串长度也不会太长，所以 在创建有序集合时，默认使用压缩列表的底层实现。zset 新插入元素时，会判断以下两种条件：

zset 中元素个数是否大于 zset_max_ziplist_entries；
插入元素的字符串长度是否大于 zset_max_ziplist_value。

当满足任一条件时，Redis 便会将 zset 的底层实现由压缩列表转为跳跃表。

if (zzlLength(zobj->ptr) > server.zset_max_ziplist_entries)
    zsetConvert(zobj,OBJ_ENCODING_SKIPLIST);
if (sdslen(ele) > server.zset_max_ziplist_value)
    zsetConvert(zobj,OBJ_ENCODING_SKIPLIST);

1
2
3
4

注意

zset 在转为跳跃表之后，即使元素被逐渐删除，也不会重新转为压缩列表。

# 五、总结

为什么选择跳跃表而不是平衡树（如 AVL、红黑树等）？

跳跃表可以在 $O(logN)$ 的时间复杂度内实现区间查找；
跳跃表相比于平衡树实现更简单，可读性好，不易出错；
跳表更加灵活，它可以通过改变索引构建策略，有效平衡执行效率和内存消耗。
跳跃表的插入和删除只需要修改相邻节点的指针，操作简单快速，而平衡树可能导致子树调整，逻辑复杂；

# 六、参考资料

《Redis 5 设计与源码分析》– 陈雷
《Redis 设计与实现》– 黄健宏
Redis内部数据结构详解(6) – skiplist (opens new window)
跳表：为什么Redis一定要用跳表来实现有序集合？ (opens new window)
深入理解跳表在Redis中的应用 (opens new window)
Redis源码阅读系列二 skipList (opens new window)

简单动态字符串 SDS 压缩列表 ZipList

鲤鱼笔记

Choose mode