数学题：规律

0204. 计数质数 (opens new window)

题目

统计所有小于非负整数 n 的质数的数量。

解析

埃氏筛：要得到自然数 n 以内的全部素数，必须把不大于根号 n 的所有素数的倍数剔除，剩下的就是素数。

代码

class Solution {
public:
    int countPrimes(int n) {
        vector<bool> is_prim(n, true);
        int ans = 0;
        int upper = sqrt(n);
        for (int i = 2; i < n; i ++) {
            if (is_prim[i]) {
                ans ++;
                if (i > upper) continue;
                for (int j = i * i; j < n; j += i) {
                    is_prim[j] = false;
                }
            }
        }
        return ans;
    }
};

0413. 等差数列划分 (opens new window)

题目

计算给定数组的所有为等差数组的子数组个数。

解析

原数组	等差数列数量	与上一数组的等差数列数量比较
$1\quad 2\quad 3$	$1$	$1-0=1$
$1\quad 2\quad 3\quad 4$	$3$	$3-1=2$
$1\quad 2\quad 3\quad 4\quad 5$	$6$	$6-3=3$
$1\quad 2\quad 3\quad 4\quad 5\quad 6$	$10$	$10-6=4$
$1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7$	$15$	$15-10=5$

通过上面表格可以看到，数组中每增加一个等差数列项，前后两等差数列数量的差值加一，进而迭代统计个数即可。

代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int ans = 0, cur = 0;
        for (int i = 2; i < nums.size(); i ++) {
            if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {
                cur ++;
                ans += cur;
            } else {
                cur = 0;
            }
        }
        return ans;
    }
};

0492. 构造矩形 (opens new window)

题目

现给定一个具体的矩形页面面积，你的任务是设计一个长度为 L 和宽度为 W 且满足以下要求的矩形的页面。要求：

1. 你设计的矩形页面必须等于给定的目标面积。
2. 宽度 W 不应大于长度 L，换言之，要求 L >= W 。
3. 长度 L 和宽度 W 之间的差距应当尽可能小。

解析

首先要保证长宽相差尽可能小，则可以从 sqrt(area) 开始尝试，不断缩小，直到能被 area 整除，此时返回即可。

代码

class Solution {
public:
    vector<int> constructRectangle(int area) {
        int w = sqrt(area);
        while (area % w != 0) {
            w --;
        }
        return vector<int>{area / w, w};
    }
};

0573. 松鼠模拟 (opens new window)

题目

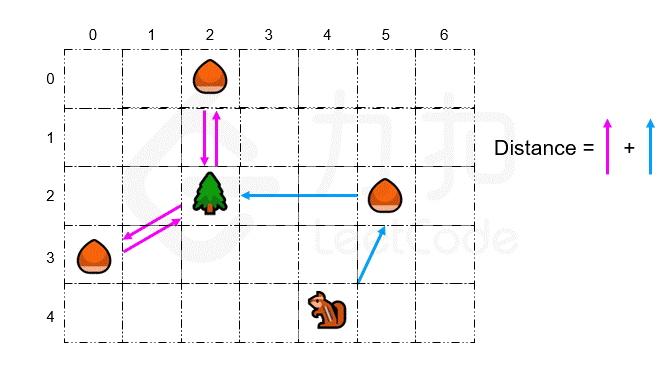
现在有一棵树，一只松鼠和一些坚果。位置由二维网格的单元格表示。你的目标是找到松鼠收集所有坚果的最小路程，且坚果是一颗接一颗地被放在树下。松鼠一次最多只能携带一颗坚果，松鼠可以向上，向下，向左和向右四个方向移动到相邻的单元格。移动次数表示路程。

解析

观察题目要求可知，除了松鼠第一次拿的坚果，所有的坚果都需要从树的位置出发，拿到坚果后再回到树的位置。也就是说，如果确定了松鼠第一次拿哪个坚果，那么答案就已经确定了。

而选择第一次拿的坚果应让“坚果-树”的距离和“坚果-松鼠”的距离的差尽可能大，这样即可得到总距离的最小值。

代码

class Solution {
public:
    int minDistance(int height, int width, vector<int>& tree, vector<int>& squirrel, vector<vector<int>>& nuts) {
        int ans = 0;
        int dist = INT_MIN;
        for (int i = 0; i < nuts.size(); i ++) {
            int dist_tree = distance(nuts[i], tree);
            ans += dist_tree * 2;
            dist = max(dist, dist_tree - distance(nuts[i], squirrel));
        }
        return ans - dist;
    }

    int distance(vector<int> a, vector<int> b) {
        return abs(a[0] - b[0]) + abs(a[1] - b[1]);
    }
};