方程组的几何解释

一、方程组的几何解释基础

线性代数的基本问题就是解 $n$ 元一次方程组。例如：二元一次方程组

$\begin{array}{cc}{2x-y=0}\\{-x+2y=3}\end{array}$

写成矩阵形式就是

$\left[{\begin{array}{cc}2&{-1}\\{-1}&2\end{array}}\right]\left[{\begin{array}{cc}x\\y\end{array}}\right]=\left[{\begin{array}{cc}0\\3\end{array}}\right]$

其中 $\boldsymbol{A}=\left[{\begin{array}{cc}2&{-1}\\{-1}&2\end{array}}\right]$ 被称为系数矩阵（coefficient matrix）。

未知数向量通常记为 $\boldsymbol{x}=\left[{\begin{array}{cc}x\\y\end{array}}\right]$。

而等号右侧的向量记为 $\boldsymbol{b}$。线性方程组简记为 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$。

1.1 二维行图像

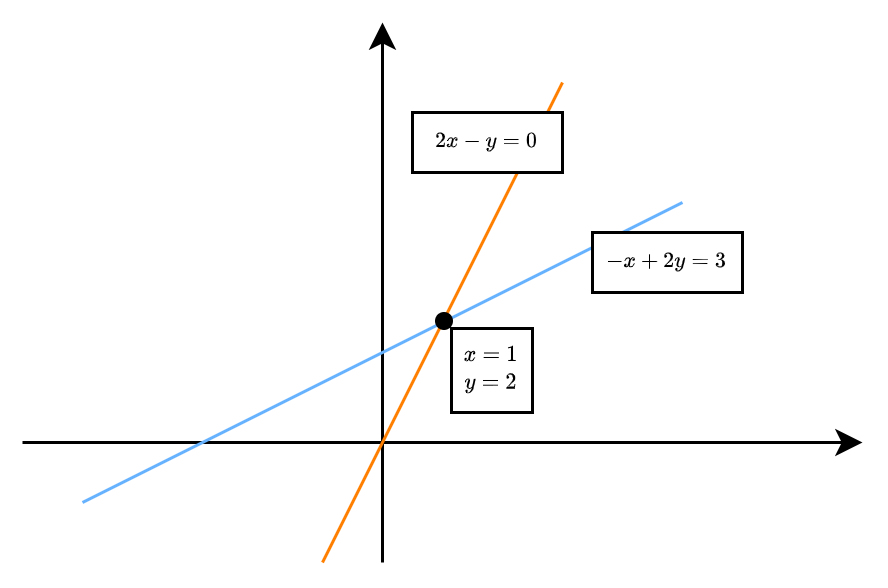
行图像遵从解析几何的描述，每个方程在平面上的图像为一条直线，两直线交点即为方程组的解 $x=1,y=2$，如下图所示。

1.2 二维列图像

在列图像中，我们将系数矩阵写成列向量的形式，则求解原方程变为寻找列向量的线性组合（linear combination）来构成向量 $\boldsymbol{b}$。

$x\left[{\begin{array}{cc}2\\{-1}\end{array}}\right]+y\left[{\begin{array}{cc}{-1}\\2\end{array}}\right]=\left[{\begin{array}{cc}0\\3\end{array}}\right]$

对于给定的向量 $\boldsymbol{c}$ 和 $\boldsymbol{d}$ 以及标量 $x$ 和 $y$，我们将 $x\boldsymbol{c}+y\boldsymbol{d}$ 称之为 $\boldsymbol{c}$ 和 $\boldsymbol{d}$ 的一个线性组合。

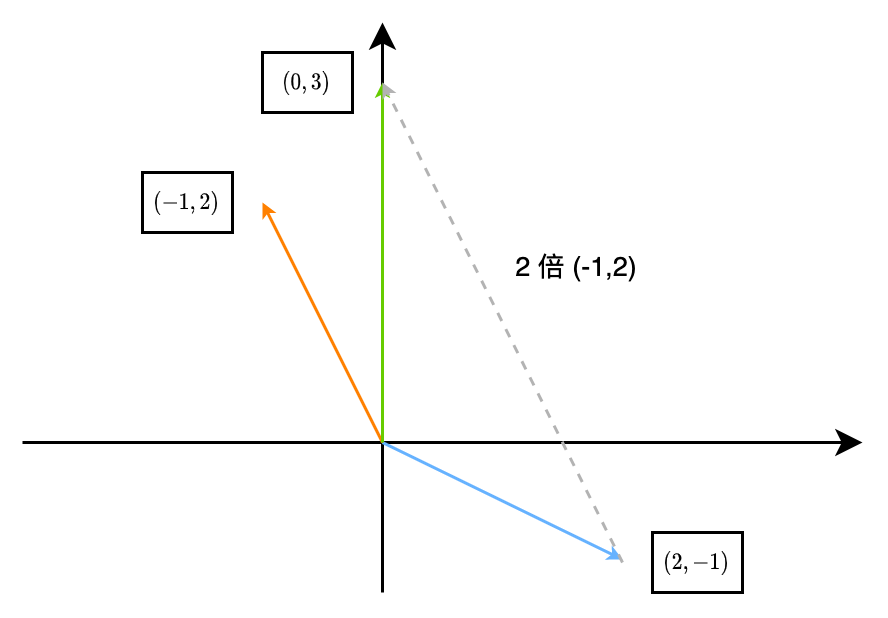
从几何上讲，我们是寻找满足如下要求的 $x$ 和 $y$，使得两者分别数乘对应的列向量之后相加得到向量 $\left[{\begin{array}{cc}0\\3\end{array}}\right]$，如下图所示。

想象一下如果任意取 $x,y$，则得到的线性组合又是什么？其结果就是以上两个列向量的所有线性组合将会布满整个坐标平面。

二、方程组的几何解释推广

将以上讨论扩展到三元

$\begin{array}{cc}x&{+2y}&{+3{\rm{z}}}&=&6\\{2x}&{+5y}&{+2z}&=&4\\{6{\rm{x}}}&{-3y}&{+z}&=&2\end{array}$

其矩阵形式为

$\left[{\begin{array}{cc}1&2&3\\2&5&2\\6&{-3}&1\end{array}}\right]\left[{\begin{array}{cc}x\\y\\z\end{array}}\right]=\left[{\begin{array}{cc}6\\4\\2\end{array}}\right]$

2.1 高维行图像

如果绘制行图像，很明显这是一个三个平面相交得到一点，我们想直接看出这个点的性质可谓是难上加难，比较靠谱的思路是先联立其中两个平面，使其相交于一条直线，在研究这条直线与平面相交于哪个点，最后得到点坐标即为方程的解。

这个求解过程对于三维来说或许还算合理，那四维呢？五维甚至更高维数呢？直观上很难直接绘制更高维数的图像，这种行图像受到的限制也越来越多。

2.2 高维列图像

相比于行图像，方程的列图像为

$x\left[{\begin{array}{cc}1\\2\\6\end{array}}\right]+y\left[{\begin{array}{cc}2\\5\\{-3}\end{array}}\right]+z\left[{\begin{array}{cc}3\\2\\1\end{array}}\right]=\left[{\begin{array}{cc}6\\4\\2\end{array}}\right]$

如果改变等号右侧的 $\boldsymbol{b}$ 的数值，那么对于行图像而言三个平面都改变了，而对于列图像而言，三个向量并没有发生变化，只是需要寻找一个新的组合。

那么问题来了，是否对于所有的 $\boldsymbol{b}$，方程 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 都有解？

从列图像上看，问题转化为 “列向量的线性组合是否覆盖整个三维空间？”

反例：若三个向量在同一平面内 —— 比如 “列 3” 恰好等于 “列 1” 加 “列 2”，而若 $\boldsymbol{b}$ 不在该平面内，则三个列向量无论怎么组合也得不到平面外的向量 $\boldsymbol{b}$。此时矩阵 $A$ 为 奇异阵 或称 不可逆矩阵。在矩阵 $\boldsymbol{A}$ 不可逆条件下，不是所有的 $\boldsymbol{b}$ 都能令方程 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$ 有解。

对 $n$ 维情形则是，$n$ 个列向量如果相互独立 —— “线性无关”，则方程组有解。否则这 $n$ 个列向量起不到 $n$ 个的作用，其线性组合无法充满 $n$ 维空间，方程组未必有解。

那么从行图像的角度来看，三元方程组是否有解意味着什么？

• 三个平面相交于一点时方程有唯一解；
• 三个平面中至少两个平行则方程无解；
• 平面的两两交线互相平行方程也无解；
• 三个平面交于一条直线则方程有无穷多解。

三、矩阵与向量的乘法

列图像：$\boldsymbol{A}\boldsymbol{x}$ 是矩阵 $\boldsymbol{A}$ 列向量的线性组合

$\left[{\begin{array}{cc}2&5\\1&3\end{array}}\right]\left[{\begin{array}{cc}1\\2\end{array}}\right]=1\left[{\begin{array}{cc}2\\1\end{array}}\right]+2\left[{\begin{array}{cc}5\\3\end{array}}\right]=\left[{\begin{array}{cc}{12}\\7\end{array}}\right]$

行图像：将矩阵 $A$ 的行向量和 $\boldsymbol{x}$ 向量进行点积来计算

$\left[{\begin{array}{cc}2&5\\1&3\end{array}}\right]\left[{\begin{array}{cc}1\\2\end{array}}\right]=\left[{\begin{array}{cc}{1\times2+2\times5}\\{1\times1+2\times3}\end{array}}\right]=\left[{\begin{array}{cc}{12}\\7\end{array}}\right]$

四、参考资料

• MIT—线性代数笔记 01 行图像和列图像 (opens new window)