栈:单调栈
# 0042. 接雨水 (opens new window)
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
解析
使用单调栈存储高度下标,按照行方向来计算雨水容量。
具体维护的顺序为从栈顶到栈底的高度有小到大,因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈顶元素就是凹槽底部的柱子,栈顶第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。这样通过左右柱子就可以计算长和宽得到雨水的容量了。
代码
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
stack<int> stk;
for (int i = 0; i < height.size(); i++) {
while (!stk.empty() && height[i] >= height[stk.top()]) {
int idx = stk.top(); stk.pop();
if (stk.empty()) break;
int w = i - stk.top() - 1;
int h = min(height[i], height[stk.top()]) - height[idx];
ans += w * h;
}
stk.push(i);
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 0084. 柱状图中最大的矩形 (opens new window)
题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
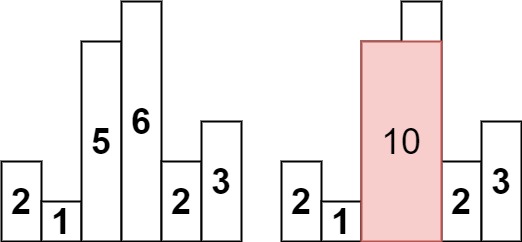
本题与 0042. 接雨水 解法相似,但由于计算面积需要找到当前柱子左右第一个比它小的柱子,因此栈内顺序与「接雨水」相反,即:从栈顶到栈底的高度右大到小,这样就可以得到当前高度的左右边界,遍历所有高度即可求出最大值。
代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> stk;
int ans = 0;
heights.push_back(-1);
for (int i = 0; i < heights.size(); i++) {
while (!stk.empty() && heights[i] < heights[stk.top()]) {
int idx = stk.top(); stk.pop();
int left = stk.empty() ? -1 : stk.top();
ans = max(ans, (i - left - 1) * heights[idx]);
}
stk.push(i);
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 0085. 最大矩形 (opens new window)
题目
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
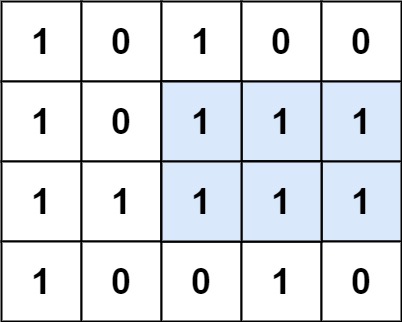
本题是 0084. 柱状图中最大的矩形 的改编版,只需在原有基础上对每一行作为 x 轴的柱状图求解即可。
代码
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<int> heights(n);
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') heights[j]++;
else heights[j] = 0;
}
ans = max(ans, maxArea(heights));
}
return ans;
}
int maxArea(vector<int>& heights) {
stack<int> stk;
int ans = 0;
heights.push_back(-1);
for (int i = 0; i < heights.size(); i++) {
while (!stk.empty() && heights[i] < heights[stk.top()]) {
int idx = stk.top(); stk.pop();
int left = stk.empty() ? -1 : stk.top();
ans = max(ans, (i - left - 1) * heights[idx]);
}
stk.push(i);
}
heights.pop_back();
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 0316. 去除重复字母 (opens new window)
题目
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
解析
本题需要维护一个保留原始相对顺序的去重单调栈,相对顺序的控制可以通过预先统计的每个字母出现次数来实现。
代码
class Solution {
public:
string removeDuplicateLetters(string s) {
vector<int> cnt(256);
for (int i = 0; i < s.length(); i++) {
cnt[s[i]]++;
}
stack<char> stk;
vector<bool> inStk(256);
for (int i = 0; i < s.length(); i++) {
cnt[s[i]]--;
// 去重
if (inStk[s[i]]) continue;
// 维护单调栈
while (!stk.empty() && s[i] < stk.top()) {
// 若后续不存在当前字符则结束
if (cnt[stk.top()] == 0) break;
inStk[stk.top()] = false;
stk.pop();
}
stk.push(s[i]);
inStk[s[i]] = true;
}
string ans = "";
while (!stk.empty()) {
ans = stk.top() + ans;
stk.pop();
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 0402. 移掉K位数字 (opens new window)
题目
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
解析
由于相同位数的数字,靠近左侧的数字越小则整体值越小,因此可以维护一个单调栈,每遇到一个较小的值都将之前入栈的元素取出,这样在取出同样位数的数字之后,保证了左侧的数字递增顺序。
有以下几个特殊情况需要处理:
- 单调栈生成之后栈内元素数超过 n - k(即:原始数字从高到低位就是近似递增的),这样需要把多余的数字 pop 出来;
- 返回结果前需要剔除前导 0(如:201,剔除 1 位后,栈内元素为 01);
- 最终结果需要对空字符串强制转 0。
代码
class Solution {
public:
string removeKdigits(string num, int k) {
stack<char> stk;
for (int i = 0; i < num.length(); i++) {
while (k > 0 && !stk.empty() && num[i] < stk.top()) {
stk.pop();
k--;
}
stk.push(num[i]);
}
// 若单调栈中元素个数超过 n - k,则进行 pop
while (k--) {
stk.pop();
}
string ans = "";
while (!stk.empty()) {
ans = stk.top() + ans;
stk.pop();
}
// 去除前导 0
ans = ans.erase(0, ans.find_first_not_of('0'));
return ans.empty() ? "0" : ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 0456. 132 模式 (opens new window)
题目
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。
解析
以中间数字 k 为基准,从后向前维护一个单调递减栈,这样确保已经找到了有效的 (j,k),同时需要记录遍历过程中 k 的最大值,这样 i 的可选范围才更大,当遇到有效的 i 时直接返回即可。
代码
class Solution {
public:
bool find132pattern(vector<int>& nums) {
int k = INT_MIN;
stack<int> stk;
for (int i = nums.size() - 1; i >= 0; i--) {
if (nums[i] < k) return true;
while (!stk.empty() && nums[i] > stk.top()) {
k = stk.top();
stk.pop();
}
stk.push(nums[i]);
}
return false;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 0496. 下一个更大元素 I (opens new window)
题目
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
解析
维护一个单调栈,记录每次遇到比栈顶元素大的值,注意只记录第一个即可。
代码
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
unordered_map<int, int> record;
stack<int> stk;
for (int i = 0; i < nums2.size(); i++) {
while (!stk.empty() && nums2[i] > nums2[stk.top()]) {
// 只记录第一个最大的,已记录过则跳过
if (record.find(nums2[stk.top()]) == record.end()) {
record[nums2[stk.top()]] = nums2[i];
}
stk.pop();
}
stk.push(i);
}
vector<int> ans(nums1.size(), -1);
for (int i = 0; i < nums1.size(); i++) {
if (record.find(nums1[i]) != record.end()) {
ans[i] = record[nums1[i]];
}
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 0503. 下一个更大元素 II (opens new window)
题目
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
解析
单调栈基础题,需要注意的是,这里用取模操作模拟了循环数组的遍历。
代码
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
vector<int> ans(nums.size(), -1);
stack<int> stk;
for (int i = 0; i < nums.size() * 2; i++) {
while (!stk.empty() && nums[i % nums.size()] > nums[stk.top()]) {
ans[stk.top()] = nums[i % nums.size()];
stk.pop();
}
stk.push(i % nums.size());
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
